CF1719B题解

分数可能是不支持的，所以用了另一种方法表示

题目大意

给你一个正偶数 \(n\) 和一个正整数 \(k\) ，要求你把这 \(n\) 个数 （从 \(1\) 到 \(n\) ）分成 \(n / 2\) 组，使得每一组的第一个数 \(a\) 和第二个数 \(b\) 满足以下条件 \((a+k)b ~\equiv~0 \pmod{4}\) 。

分析

考虑分类讨论。

当 \(k \equiv 0 \pmod {4}\) 时，显然不可以满足条件。因为这时原式等价于 \(ab ~\equiv~0 \pmod{4}\) ，就使得每个奇数都要配上一个 \(4\) 的倍数，但是奇数的个数 \(n / 2\) 是高于 \(4\) 的倍数的个数 \(\lfloor n / 4 \rfloor\) 的，所以无法配对。

当 \(k \equiv 2 \pmod {4}\) 时，原式等价于 \((a+2)b ~\equiv~0 \pmod{4}\) ，这时只要满足以下两个条件的一种就行了：\(a\) 是奇数，\(b\) 是 \(4\) 的倍数或 \(a\) 是非 \(4\) 倍数的偶数， \(b\) 是奇数即可。

以上很好解释，但构造的方法是什么呢？

可以考虑蛇形构造，如下图：

构造方法

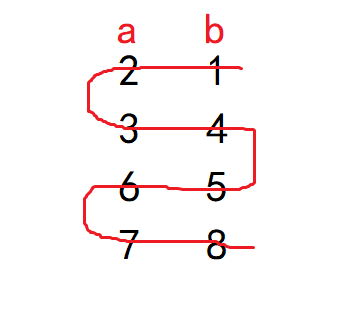
当 \(k \equiv 1 \pmod {4}\) 或 \(k \equiv 3 \pmod {4}\) 时，原式等价于 \((a+1)b ~\equiv~0 \pmod{4}\) 或 \((a+3)b ~\equiv~0 \pmod{4}\) ，这时只要保证 \(a\) 是奇数， \(b\) 是偶数即可，构造直接顺序输出。

代码就不用注释了吧。

void wk() {
    int n,k;
    read(n),read(k);
    if(!(k&3)) {
        printf("NO\n");
        return ;
    }
    printf("YES\n");
    if(k&3==1 || k&3==3) {
        for(int i=1;i<=n;i+=2) {
            write(i),putchar(32),write(i+1),putchar(10);
        }
    }
    else {
        for(int i=1,j=1;i<=n;i+=2,++j) {
            if(j&1) write(i+1),putchar(32),write(i),putchar(10);
            else write(i),putchar(32),write(i+1),putchar(10);
        }
    }
}